문제
요즘 많은 자동차에서는 GPS 네비게이션 장비가 설치되어 있다. 네비게이션은 사용자가 입력한 출발점과 도착점 사이의 최단 경로를 검색해 준다. 하지만, 교통 상황을 고려하지 않고 최단 경로를 검색하는 경우에는 극심한 교통 정체를 경험할 수 있다.
상근이는 오직 자기 자신만 사용 가능한 네비게이션을 만들고 있다. 이 네비게이션은 절대로 최단 경로를 찾아주지 않는다. 항상 거의 최단 경로를 찾아준다.
거의 최단 경로란 최단 경로에 포함되지 않는 도로로만 이루어진 경로 중 가장 짧은 것을 말한다.
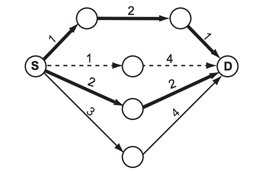
예를 들어, 도로 지도가 아래와 같을 때를 생각해보자. 원은 장소를 의미하고, 선은 단방향 도로를 나타낸다. 시작점은 S, 도착점은 D로 표시되어 있다. 굵은 선은 최단 경로를 나타낸다. (아래 그림에 최단 경로는 두 개가 있다)거의 최단 경로는 점선으로 표시된 경로이다. 이 경로는 최단 경로에 포함되지 않은 도로로 이루어진 경로 중 가장 짧은 경로이다. 거의 최단 경로는 여러 개 존재할 수도 있다. 예를 들어, 아래 그림의 길이가 3인 도로의 길이가 1이라면, 거의 최단 경로는 두 개가 된다. 또, 거의 최단 경로가 없는 경우도 있다.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 장소의 수 N (2 ≤ N ≤ 500)과 도로의 수 M (1 ≤ M ≤ 104)가 주어진다. 장소는 0부터 N-1번까지 번호가 매겨져 있다. 둘째 줄에는 시작점 S와 도착점 D가 주어진다. (S ≠ D; 0 ≤ S, D < N) 다음 M개 줄에는 도로의 정보 U, V, P가 주어진다. (U ≠ V ; 0 ≤ U, V < N; 1 ≤ P ≤ 103) 이 뜻은 U에서 V로 가는 도로의 길이가 P라는 뜻이다. U에서 V로 가는 도로는 최대 한 개이다. 또, U에서 V로 가는 도로와 V에서 U로 가는 도로는 다른 도로이다.
입력의 마지막 줄에는 0이 두 개 주어진다.
출력
각 테스트 케이스에 대해서, 거의 최단 경로의 길이를 출력한다. 만약, 거의 최단 경로가 없는 경우에는 -1을 출력한다.
풀이
import java.io.*;
import java.util.*;
public class Main {
static final int MAXN = 500;
static final int INF = Integer.MAX_VALUE;
static BufferedReader br;
static StringTokenizer st;
static StringBuilder sb;
static int[][] adj;
static int[] dp;
static int n, m, s, d, from, to, w;
public static void main(String[] args) throws IOException {
br = new BufferedReader(new InputStreamReader(System.in));
sb = new StringBuilder();
adj = new int[MAXN][MAXN];
dp = new int[MAXN];
while (true) {
st = new StringTokenizer(br.readLine());
n = stoi(st.nextToken());
m = stoi(st.nextToken());
if(n == 0 && m == 0) break;
for(int[] arr : adj) {
Arrays.fill(arr, 0);
}
st = new StringTokenizer(br.readLine());
s = stoi(st.nextToken());
d = stoi(st.nextToken());
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
from = stoi(st.nextToken());
to = stoi(st.nextToken());
w = stoi(st.nextToken());
adj[from][to] = w;
}
dijkstra(s);
removeShortest(d);
dijkstra(s);
sb.append(dp[d] == INF ? -1 : dp[d]).append("\n");
}
System.out.print(sb);
}
static void dijkstra(int s) {
Arrays.fill(dp, INF);
PriorityQueue<Route> pq = new PriorityQueue<>(((o1, o2) -> o1.w - o2.w));
pq.add(new Route(s, 0));
dp[s] = 0;
while(!pq.isEmpty()) {
Route cur = pq.poll();
//현재 최단경로의 정점과 연결된 경로 순회
for (int i = 0; i < n; i++) {
//연결 안되어 있거나 이미 최단경로가 있는데 더 작은경우는 안봐도 됨
if(adj[cur.v][i] == 0 || adj[cur.v][i] > dp[i]) continue;
//현재의 경로로 갱신해야 한다면
int nextWeight = adj[cur.v][i] + dp[cur.v];
if(nextWeight < dp[i]) {
dp[i] = nextWeight;
pq.add(new Route(i, dp[i]));
}
}
}
}
static void removeShortest(int d) {
Queue<Integer> q = new LinkedList<>();
q.add(d);
while(!q.isEmpty()) {
int cur = q.poll();
for (int to = 0; to < n; to++) {
//해당 경로가 최단경로 라면
if(adj[to][cur] != 0 && dp[cur] == adj[to][cur] + dp[to]) {
//삭제
adj[to][cur] = 0;
//큐에 삽입
q.add(to);
}
}
}
}
static int stoi(String s) {return Integer.parseInt(s);}
}
class Route {
int v;
int w;
public Route(int v, int w) {
this.v = v;
this.w = w;
}
}다익스트라의 기본 응용 문제였다.
두번째 최단경로를 찾으면 되는 문제이다. 따라서 첫번 째로 찾은 최단경로를 알맞게 제거해주고 다시 한번 최단경로를 찾아주면 두번 째 최단경로가 나오게 된다.
'Dev > PS' 카테고리의 다른 글
| [백준] 1922 네트워크 연결 java (0) | 2022.08.09 |
|---|---|
| [백준] 11660 구간 합 구하기 5 (0) | 2022.08.09 |
| [백준] 1753 최단경로 java (0) | 2022.08.05 |
| [백준] 2252 줄 세우기 java (0) | 2022.07.26 |
| [백준] 9663 N-Queen java (0) | 2022.07.23 |
